Desafortunadamente ha llegado el momento de someteros al trago de otra entrega de la serie de los Alienígenas matemáticos, que tantos daños ha producido en la psique de sus lectores. Si tienes la suerte de no conocer esta serie, no sigas leyendo. Continúa viviendo en el mundo confortable y racional de la geometría riemanniana y cuatro humildes dimensiones. Como debería ser obvio por este mismo párrafo, esta serie es inútil, verborreica, pedante, y cualquier otro uso de tu tiempo –como por ejemplo ver comer a los caracoles– es mucho más provechoso. ¡Hasta luego!
Por supuesto, sub-criatura, sabía que tú seguirías leyendo, lo cual dice más sobre ti que sobre mí. En fin. Te recuerdo que esta serie es densa, requiere pensar bastante y, en mi opinión, se saca más provecho de ella y se disfruta más si coges lápiz y papel y paras de vez en cuando para dibujar, calcular y pensar. En eso consiste: en estimular tu patético intelecto. Si no la conoces, es absurdo que leas este artículo sin haber sufrido antes los anteriores, así que yo me dirigiría al índice y empezaría por el principio. Me lo agradecerás después.
El caso es que hoy hablaremos sobre cómo el infame Nesretlimorb Retep, un criminal Alienígena de la peor especie, consiguió la libertad junto con sus compañeros –varios de los cuales se unirían a él para formar una banda criminal de terrible reputación– utilizando su brillantísima mente, más afilada aún que sus colmillos. Este cuento cuenta además con un par de ilustraciones de Pedro Criado, el primer humano en osar poner cara a los Alienígenas Matemáticos. Allá él.
Nesretlimorb había alcanzado la notoriedad –que no la fama– tras varios crímenes espantosos, entre los que se incluía el peor de todos: mostrar misericordia a una especie recién descubierta, aunque eso es otra historia y tendrá que esperar a otra ocasión. Los crímenes de este monstruo habían sido tan elegantes y llevados a cabo con tal astucia que, como sucede a veces, en vez de ser ejecutado Nesretlimorb Retep fue encarcelado en una prisión de máxima seguridad, la famosísima de Tau Ceti. Esta prisión era conocida en todo el Brazo de Orión por la crueldad y soberbia (dos magníficas cualidades para los Alienígenas) de su carcelero, Muyksnevs, y contenía un millón de presos (la mayor de todo el Sector Galáctico), todos ellos numerados del 1 al 1 000 000. Nunca se admitía un preso nuevo hasta haber una vacante, claro.
Como toda prisión Alienígena, por tradición, la de Tau Ceti tenía una manera pública de ganar la libertad. Pero, dados incidentes tan bochornosos como el de la Prisión de Loobe, el Carcelero Muyksnevs se había guardado muy bien de proporcionar una posibilidad real de escapatoria: había diseñado un reto cuya probabilidad de éxito no era nula (lo cual hubiera sido una trampa), pero a efectos prácticos el resultado era indistinguible de ese. Durante los tres siglos y medio que había existido la prisión de Tau Ceti, no ya es que ningún prisionero hubiera obtenido la libertad, sino que ninguno se había atrevido siquiera a jugar al reto de Muyksnevs (ya que, en esta sociedad, perder un juego tiene una consecuencia letal).
Hasta dos días después de que llegase a ella el héroe de nuestra historia de hoy, Nesretlimorb Retep, claro. Todo empezó cuando Retep (prisionero #774212) preguntó al prisionero de la celda contigua (prisionero #774213) sobre las reglas del obsceno juego de Muyksnevs.
“Es inútil, no hay escapatoria”, le dijo #7742128568583, un Lémur de Magallanes, mirándolo con ojos enormes y tristes. “Muyksnevs afirma que nos deja una posibilidad, pero es todo una artimaña. No hay escapatoria”, repitió.
Nesretlimorb lo observó con interés –y sin apetito, ya que como digo era un Alienígena inusual en muchos aspectos, aunque no en su talento matemático– con varios de sus ojos. “Pero, ¿en qué consiste el juego?”, preguntó con voz rasposa.
“El juego tiene dos partes, una individual y otra grupal”, respondió el Lémur. “En la individual, el preso que está jugando se enfrenta a un millón de cajas marcadas con números de 1 a 1 000 000, como los prisioneros. En el interior de cada caja –de modo que solo pueda verse al abrirla– hay un número pintado, del 1 a 1 000 000, como antes, que no tiene por qué coincidir con el número de fuera, claro, porque han sido asignados aleatoriamente.”

Algunas de las cajas del juego de Muyksnevs.
Nesretlimorb asintió pacientemente: los Lémures eran gentiles, pero no las criaturas más avispadas ni rápidas de la Galaxia. “Un millón de cajas numeradas, con un millón de números dentro. Entendido. ¿Y el juego?”
“El jugador puede abrir 900 000 cajas. Y gana si alguna de ellas contiene su propio número de presidiario. Si yo jugase…”, dijo mientras tragaba saliva, ”… ganaría el juego de abrir la caja en cuyo interior estuviera el número 774213, mi número asignado.”
“No parece un juego muy difícil de ganar…”, afirmó el enorme y batrácico Alienígena, que sabía perfectamente que un monstruo de la talla de Muyksnevs no dejaría las cosas tan fáciles.
“¡No! Al abrir el 90% de las cajas, la probabilidad de abrir la que contiene tu número es… ¡del 90%!”, exclamó con voz aguda el pequeño #774213, mientras su baboso y gigantesco interlocutor asintía con gran paciencia. “Pero eso es solo para el juego individual…”
“¿Y el grupal?”, preguntó Nesretlimorb con voz húmeda y acariciadora.
“¡Ahí está el truco!”, dijo el Lémur. “El maligno Muyksnevs se jacta de su generosidad por el 90%, pero el juego es de grupo. Un prisionero no puede enfrentarse a su reto para salir libre, ¡tenemos que decidir jugar todos, un millón de nosotros, uno tras otro! Y ese maldito ikkkikkyk (una palabra Lémur intraducible, que reproduce el sonido de un bebé Lémur siendo devorado por un depredador nocturno) dice que, o nos salvamos todos, o perdemos todos. Y para ganar tienen que ganar el juego todos los jugadores. Si uno solo pierde, perdemos todos. Y no podemos hablar unos con otros durante el juego para decirnos nada sobre las cajas, claro. Y perder el juego significa…”
Nesretlimorb gorgoteó profundamente. “Perder la vida, obviamente. Ya veo”, asintió abriendo y cerrando varios de sus ojos secundarios.
El Lémur estaba ahora muy agitado, y como había pensado en esto muchas veces –como todos los prisioneros– estaba encantado de demostrar su razonamiento. “Imaginemos que fuésemos diez prisioneros”, dijo moviendo las orejillas. “Diez prisioneros, diez cajas, y cada uno que juega puede abrir nueve de las diez cajas… su probabilidad de ganar es del 90% individualmente, claro.”
“Pero todos deben tener éxito”, interrumpió Nesretlimorb, azuzando al otro.
¡Claro! ¡Y ahí está el problema!, exclamó el Lémur agitando su cola anillada. “Si uno de los diez fracasa, todo se va al garete, luego la probabilidad total no es un 90%, sino el 90% del 90% del 90%… y así diez veces. Y 0,9x0,9x…x0,9 diez veces es…”
“El 34,867844%”, apuntó el Alienígena Matemático haciendo honor a su especie.
“¡Y eso es solo con diez prisioneros! Con cien, por ejemplo, la cosa se vuelve ya desoladora, la probabilidad de que ninguno fracase es de 0,9 elevado a 100, que supo…”
“0,00265614%”, le interrumpió el monstruo sin apenas levantar la voz. “Entiendo el problema”.
“Y para un millón…”, terminó #774213 lastimosamente. *“La probabilidad de éxito es 0,9 elevado a un millón, que es.. que es…”
Nesretlimorb tardó dos segundos y medio en calcularlo, lo cual te da una idea de lo largo de la operación. “$3,2317610\cdot10^{-45758}$”, dijo finalmente. “Es decir, tan cerca de cero que es imposible la salvación.”
Una enorme y prístina lágrima se derramó de uno de los grandes ojos del Lémur y cayó en silencio al suelo. “Ya dije que no hay esperanza…”
“En absoluto, mi pequeño, peludo y probablemente tierno amigo”, respondió Nesretlimorb, produciendo en el otro un pánico instintivo, acentuado incluso por la amabilidad del tono del monstruo. Nunca hubiera pensado el Lémur que un Alienígena pudiera hablar así, pero como digo Nesretlimorb era especial en muchas cosas. “Tengo una estrategia que proporciona al conjunto alrededor de un 89% de éxito, tan solo un poco menor probabilidad que la individual.”
“¿¡Có… cómooo?!”, exclamó el Lémur, tembloroso. “Pero si cada jugador tiene una probabilidad menor que 1 de tener éxito, cada uno que juega disminuye la probabilidad final, ¡y somos un millón!”
Pero el cuerpo de Nesretlimorb se estremecía con un placer lascivo mientras discurría y confirmaba que su estrategia era correcta, tras probarla una y otra vez en su magnífica y bulbosa cabeza. Los tentáculos se agitaban como anguilas en una tormenta, y regueros de babas caían de su boca, creando pequeños agujeros en el cemento del suelo. El monstruo, extático, empezó a reír. Imagino que nunca has escuchado reír a un Alienígena Matemático, pero es algo que produce pesadillas. #774213, en una montaña rusa de emociones, empezó a sollozar desconsolado.

“Llama al prisionero #1, y cuando todos los prisioneros estén de acuerdo (que lo estarán en cuanto les explique mi estrategia), avisa al carcelero de que mañana…”, ordenó con un ronroneo amenazador Nesretlimorb (que era un Alienígena inusual, pero un Alienígena al fin y al cabo). ”… jugamos con Muyksnevs.”
Antes de que sigas leyendo, primate, te recomiendo que intentes pensar en alguna estrategia que mejore la aleatoria del Lémur: puedes empezar con diez prisioneros, que hace todo más adecuado a las limitaciones de tu patética, quiero decir, de nuestra patética especie. No sé si alcanzarás el genio de Nesretlimorb (bueno, sí lo sé), pero pensar es divertido hasta para los homínidos.
…
…
…
…
…
…
…
…
…
Dos días más tarde, terminado el juego, Nesretlimorb se encontraba en el despacho del carcelero mayor, Muyksnevs (que sudaba sustancias tóxicas y volátiles que llenaban la habitación de olores nauseabundos), mientras el Subdirector General de Prisiones era testigo de la liberación masiva de un millón de prisioneros: algo nunca visto en la larguísima historia de los Alienígenas Matemáticos.
“¡Es imposible!”, exclamó, con un rugido ensordecedor y soltando espumarajos, Muyksnevs, mientras miraba a Nesretlimorb con ojos que destilaban odio, miedo y repugnancia –dependiendo del racimo de ojos–. “Ha habido alguna trampa, ¡no puede ser! ¡La probabilidad es tan pequeña que no puede haber sucedido!”
“El desarrollo del juego está completamente controlado por usted para que los prisioneros no puedan hacer trampa, como usted sabe, carcelero”, respondió con tranquilidad y voz felina el Subdirector General. “Estoy seguro de que al prisionero #774212… perdón, quiero decir, al ex-prisionero #774212, no le importará explicarnos cómo ha razonado para vencer este juego aparentemente imposible”.
“Por supuesto”, respondió Nesretlimorb, agitando levemente algunos tentáculos con placer. “El error de mis predecesores había consistido en tratar un problema colectivo –ya que todos nos salvaríamos juntos o pereceríamos juntos– como una suma de problemas individuales –ganar o perder probabilísticamente el juego uno tras otro–. Lo que era necesario era asociar las probabilidades, de modo que no fuesen independientes unas de otras. Conseguir que si un jugador ganaba, eso significase que los demás tendrían más probabilidades de ganar y no menos”.
“¡IMPOSIBLE!”, exclamó Muyksnevs. “¡Imposible!”, repitió, demostrando poca originalidad. Los otros dos lo miraron, arqueando varias cejas –trece en un caso, siete en el otro–, pero el carcelero no supo seguir: se quedó, tembloroso y babeante, esperando la explicación de Nesretlimorb.
El ex-prisionero hizo ronronear varios de sus páncreas, saboreando el momento. “Dado que cada caja tiene fuera el número de un prisionero, y dentro el número de otro –o el mismo, por supuesto, pero uno solo–, hay una relación de uno a uno entre ambos números, fuera y dentro. De modo que la solución fue muy simple: cada prisionero debía abrir en primer lugar la caja que mostrase su propio número, mirar el que hubiera dentro y abrir esa caja, mirar el número que hubiese dentro, abrir esa caja, y así sucesivamente hasta abrir novecientas mil cajas o encontrar la suya, claro. Así de simple: así indiqué al prisionero #1, que se lo explicó al #2, este al #3, etc. Todos lo entendieron perfectamente. Incluso los humanos.”
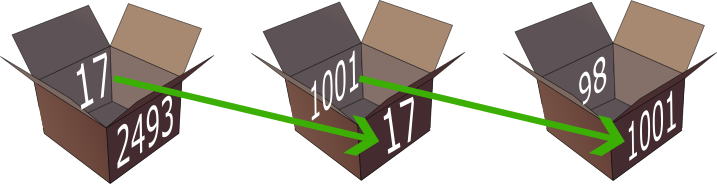
La estrategia de Nesretlimorb.
“¿Y por qué eso es diferente de abrir novecientas mil cajas al azar?”, preguntó con interés el Subdirector General.
“Por los bucles”, respondió Nesretlimorb. “La relación de uno a uno entre números exteriores e interiores hace que, si se sigue la cadena que he dicho, necesariamente uno vuelve a la caja inicial tarde o temprano. Por ejemplo, la caja 326 puede tener dentro el número 461, esa el 1002, esa el 3, y esa última el 326. Es inevitable que esto suceda antes o después: las cajas, siguiendo este sistema, siempre forman un bucle cerrado que termina en la inicial.”
Los otros dos monstruos, aunque no tuvieran la talla intelectual de Nesretlimorb Retep, asintieron con la cabeza casi inmediatamente.
“De no cumplirse esto,” continuó la criatura, “algún número debería repetirse y algún otro faltar. Teniendo un millón de cajas numeradas del 1 al 1 millón, con los mismos números en cualquier orden dentro de cada una, el camino iniciado según mi sistema no puede tener ramificaciones. De modo que, ¿dónde acabaría? Si terminase en la caja 256, ¿qué número hay en esa caja? ¿Ninguno? Luego el camino no puede tener principio ni fin: debe ser un bucle.”
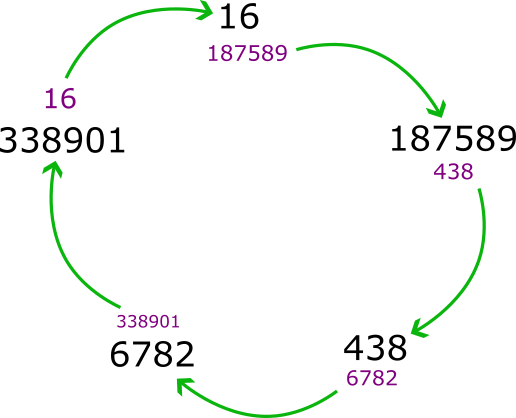
Un bucle de cinco cajas.
El Subdirector General y el carcelero lo escuchaban, embobados: el primero era recorrido por oleadas de colores pastel, fruto de un placer intelectual obsceno, y el segundo por fogonazos rojos y amarillos, cáusticos y reveladores de una furia y terror in crescendo.
“Ahora bien, ¿cuántos bucles y cómo de grandes? Esa es la cuestión”, continuó Nesretlimorb. “Podría por ejemplo haber un solo bucle, la situación más simple posible: el millón de cajas conectadas una con la siguiente, esa con la siguiente, hasta que se volviese a la primera. En ese caso, mi sistema naturalmente llevaría al fracaso: abriendo novecientas mil cajas una tras otra no se cerraría el bucle, y no solo un prisionero perdería el juego, ¡lo hubiésemos perdido todos!” Aquí Muyksnevs tragó saliva, desasosegado, algo que el ex-prisionero no dejó de notar, por supuesto.
“El caso contrario, muy favorable a mi estrategia, sería que hubiese muchos bucles muy pequeños: por ejemplo, parejas. La caja 2469 apunta a la 987, y la 987 a la 2469. Todos los prisioneros hubieran ganado el juego individual tras abrir dos cajas. Pero esto, como el caso anterior, es muy improbable.”
“Entonces,”, apuntó el Subdirector General, “si lo he entendido bien, todo depende de la longitud de los bucles. Un prisionero que abriese la caja con su número, y luego la marcada con el número interior, y así sucesivamente, tiene garantizado volver a la suya por la relación de uno a uno entre unos números y otros. Lo que determina entonces que gane o pierda es cómo de largo es el bucle: si tiene hasta 900 000 cajas, habrá ganado, y si tiene más, habrá perdido, y por tanto habrán perdido el juego de manera colectiva todos los presos”.
“Y por ende,” asintió Nesretlimorb, “el éxito o el fracaso depende de la longitud del bucle más largo. Si ese bucle es más largo que 900 000, todos los presos de ese bucle fracasarán y los prisioneros habrán perdido el juego. Si, por el contrario, el bucle más largo es menor de 900 000 elementos, todos los presos estarán en bucles que podrán completar antes de agotar las cajas que pueden abrir, y todos tendrán éxito. La clave de mi estrategia es, por tanto, asociar las probabilidades de éxito para que cada prisionero adicional no disminuya necesariamente la probabilidad total, porque todos los que comparten bucle ganan o pierden como uno.”
Mientras las otras dos criaturas hablaban, el cada vez más pálido Muyksnevs miraba a ambos simultáneamente con sus ojos reptiloides. Un leve olor a amoníaco empezó a llenar la sala.
“Todo esto significa”, continuó el ex-preso #774212 cada vez más animado, “que el problema se reduce a calcular cuál es la probabilidad de que, con números asignados aleatoriamente,” y aquí el carcelero no pudo reprimir un leve temblor de sus tentáculos, “exista algún bucle con una longitud mayor de 900 000. Y eso es trivial calcularlo, pero lo haré de todos modos simplemente por disfrutarlo.”
El Subdirector asintió, complacido. Muyksnevs se mantuvo en un tenso silencio de pánico contenido.
“Como hay un millón de cajas numeradas y un millón de números por asignar, el total de posibilidades es el número de permutaciones de ese millón de elementos, ya que con las cajas en orden (1, 2, 3…) podrían asignarse los números (1, 2, 3…) en cualquier orden a ellas. Es decir, el número de casos posibles es 1 000 000!, el factorial de un millón. Un número bastante grande, por supuesto.”
“El fracaso se produce entonces si ahí hay algún bucle de más de 900 000 elementos: pero solo puede haber uno como máximo, ya que de haberlo, el resto de cajas serían menos del 10% de las totales. Luego basta con calcular qué probabilidad existe de que una de esas permutaciones tenga más de novecientos mil elementos en un bucle. Para eso hay que calcular cuántas posibilidades hay de tener un bucle de esa longitud.”
“Empecemos con el caso más fácil: la probabilidad de que exista un bucle de un millón de cajas, es decir, el peor caso posible para los prisioneros. Es una probabilidad muy pequeña, claro. Como el millón de cajas está en una secuencia, las posibles permutaciones son las mismas que antes: el factorial de un millón…”
“¡Pero algunas estarán repetidas!”, apuntó Muyksnevs rápidamente. Los otros dos lo miraron con cierto desprecio.
”… pero, como indica el perspicaz carcelero, como son bucles, no hay comienzo ni fin y muchas son equivalentes: 1->3->5 y 5->3->1, dado que el último número apunta al primero, son realmente el mismo bucle. La diferencia entre esas permutaciones sería por tanto simplemente dónde empezaron, y como hay un millón de cajas, habría un millón de posibilidades de dónde empezar ese bucle máximo. Por lo tanto, los casos favorables de este bucle son en la práctica el factorial de un millón dividido por un millón de bucles equivalentes: $\frac{1000000!}{1000000}$”.
El Subdirector asintió. “Y teniendo los casos favorables a ese bucle y los casos posibles, podemos obtener la probabilidad de que exista un bucle de longitud máxima:”
“Efectivamente, una probabilidad de uno entre un millón. Y en ese porcentaje de casos, los prisioneros perderían. Pero claro, también pierden si el bucle más largo es de 999 999 cajas. ¿Y cuál es la probabilidad de que eso suceda? El argumento es exactamente el mismo: existen 999 999! maneras de conseguir una secuencia de 999 999 cajas, pero 999 999 de ellas serán bucles idénticos salvo por el inicio, que es irrelevante, luego realmente son $\frac{999999!}{999999}$.”
“Entiendo. Y la probabilidad de que eso suceda es el cociente entre ese número de casos y el total de ordenaciones posibles de 999 999 cajas, es decir:”
“Que es algo mayor, por supuesto, ya que es una condición menos exigente”, confirmó Nesretlimorb Retep. “Y la probabilidad conjunta, ya que son casos mutuamente excluyentes, es simplemente la suma:”
“¡Sí, sí, y el siguiente caso tendrá una probabilidad de $\frac{1}{999998}, obviamente!$”, espetó Muyksnevs soltando espumarajos. “¡Ya sabemos a dónde quiere llegar, así que termine de una vez!”
“Por supuesto”, respondió Nesretlimorb sonriendo con múltiples hileras de dientes afilados como cuchillas. “Habría que seguir haciendo lo mismo hasta llegar a la probabilidad de un bucle máximo de 900 001 cajas, el primero en el que los prisioneros pierden. Y la suma de todas esas probabilidades es:”
“¡Una probabilidad que cualquier recién nacido puede calcular fácilmente: 0,10536046, es decir, el 10,54% nada más!, exclamó, algo sorprendido, el Subdirector General. “Y por lo tanto la probabilidad de éxito de los prisioneros es la restante, el 89,46%. ¡Brillante!”
Nesretlimorb asintió con cierta modestia (pero no mucha, porque era un Alienígena inusual, pero no tanto). “La clave está en que, siguiendo mi estrategia, en la mayor parte de los casos todos los presos tienen éxito, y en un pequeño porcentaje no solo fracasa alguno, sino que fracasan al menos el 90% de ellos. Es un modo de agrupar los éxitos juntos en vez de tenerlos dispersos en una distribución normal, como sucede al abrir 900 000 cajas al azar, y…”
“¡IMPOSIBLE! ¡Todo es una falacia, una argucia, su Vileza!”, gritó, con voz quebrada, el carcelero. “¡Todo lo que ha calculado esta sibilina criatura es correcto, pero no garantiza el éxito, hay más de un 10% de probabilidad de fracaso si existe un bucle mayor… y aquí existía un bucle más largo, ¡porque lo asigné secretamente yo mismo la noche anterior!”
La piel del Subdirector General cambió de color y textura como la de un pulpo: se llenó de pinchos y se tintó de colores rojos, negros y blancos. Un intensísimo olor a amoníaco se desprendió de múltiples glándulas bajo cada tentáculo. Muyksnevs acababa de admitir un delito –hacer trampa en un juego matemático– que solo tenía un castigo: la muerte y consumición, afortunadamente en ese orden. Era un delito tan horrible que el Subdirector se quedó parado unos segundos, horrorizado. Pero Nesretlimorb simplemente asintió con la cabeza con tranquilidad.

“Claro, todos mis cálculos funcionan considerando una distribución aleatoria de los números, que era la regla establecida. Pero había una posibilidad de que el organizador del juego, por si acaso, hubiera distribuido los números intencionadamente con un bucle que garantizase perder el juego. En este caso esa posibilidad era grande, dado lo mediocre del organizador. Yo la estimé en un 64,4%”, concluyó el monstruó pensativamente. “Y nos protegí de ella.”
“¿Cómo?”, preguntó el Subdirector, admirado, mientras Muyksnevs retorcía sus tentáculos con impotencia. Dos guardias, tras un gesto del Subdirector, se habían aposentado ya a ambos lados del carcelero.
“Sumando una cantidad aleatoria pero fija (en este caso elegí 130) al número obtenido de cada caja. Por ejemplo, si un prisionero abría una caja y dentro estaba el 100, en vez de abrir la caja número 100, el prisionero abriría la 230. Si el número fuese el 999 999, volvería a contar desde el principio, es decir, el 999 999 + 130 = 129. Esto equivale, a efectos prácticos, a reordenar los bucles aleatoriamente de modo que incluso si alguien fuera tan despreciable, tan débil, tan… mediocre”, y ante ese insulto máximo el resto de Alienígenas de la sala contuvieron la respiración mientras Muyksnevs se tornaba blanco como la cal, “como para trucar el juego, incluso así la probabilidad de nuestro éxito seguiría siendo del 89,46%.”
“Una estrategia realmente notable”, asintió el Subdirector General. “Creo que está claro lo que debemos hacer”.
Unas horas más tarde, Nesretlimorb y el Subdirector cenaban tranquilamente en un comedor privado.
“Un poco duro”, comentó el Subdirector.
“Es el pánico continuado, contrae mucho los músculos. Debería haber esperado a revelar el secreto hasta el final para que no lo aguantase tanto”, suspiró Nesretlimorb, dando otro bocado.
En el problema original hay cien prisioneros, y no un millón, pero ese número es mucho más adecuado para los Alienígenas Matemáticos, y el número de cajas que pueden abrir es de 50, es decir, la mitad del total, en vez del 90%. Pero modifiqué eso segundo porque con un 50% de cajas la probabilidad de éxito de los prisioneros era solo del 31%, y el 90% (casi la misma que la de un prisionero individual) me parece mucho más satisfactoria. Además, es más ajustada al carácter de Muyksnevs, que se jactaba de ser generoso con su 90% mientras la probabilidad total era del 0% en la práctica. Pero puedes leer la versión original, mejor explicada y sin idioteces, en los enlaces a continuación.
Para saber más: