Hoy continuamos con la traducción comentada de los Discorsi de Galileo, el libro que estableció varias de las bases de la física moderna y sirvió de trampolín a Newton. Si llegas aquí de nuevas, lo mejor es que empieces desde el principio.

Habíamos dejado a Salviati, Sagredo y Simplicio discutiendo sobre el infinito: infinitos volúmenes infinitamente pequeños constituyendo los espacios interiores de la materia, con vacíos diminutos e innumerables manteniéndola unida –una noción falsa, pero fascinante–.

El obstáculo en la discusión es el propio concepto de infinito, que antes del italiano no había recibido demasiada atención en Occidente. Pero Galileo se dedica a examinarlo con el detalle del que es capaz en el siglo XVII. Ojo, porque hoy hace falta cierto grado de visión espacial y algo de geometría, pero no te preocupes porque iremos de la mano con figuras auxiliares que los lectores originales no tenían.

Como siempre, dejo la última intervención del fragmento anterior para luego seguir:

Salviati – Estos obstáculos son reales, y no son los únicos. Pero recordemos que estamos tratando con infinitos e indivisibles, los cuales trascienden nuestra comprensión finita, los primeros por su enormidad y los segundos por su pequeñez. A pesar de esto los hombres no pueden evitar discutir sobre ellos, incluso si deben hacerlo con rodeos.

Por lo tanto, también me gustaría tomarme la libertad de presentaros algunas de mis ideas, las cuales, aunque no sean necesariamente convincentes, deberían ser interesantes por su novedad. Pero una digresión de este tipo tal vez nos lleve demasiado lejos del asunto que estamos discutiendo, y puede pareceros por lo tanto inoportuna y desagradable.

Sagredo – Por favor, deja que disfrutemos de las ventajas y privilegios de la conversación entre amigos, especialmente de asuntos libremente elegidos y no forzados sobre nosotros, algo completamente distinto de leer libros muertos que hacen surgir muchas dudas y no resuelven ninguna. Comparte con nosotros, por lo tanto, las ideas que te ha sugerido nuestra discusión. Ya que no tenemos asuntos urgentes que atender, tendremos tiempo de sobra para volver a los asuntos antes mencionados; en particular, no sería buena idea obviar las objeciones de Simplicio.

Lo mejor de este párrafo, aunque puede pasar desapercibido, es lo de leer libros muertos. Galileo se refiere a algo que lo irrita muchísimo: a la tendencia de los eruditos de su época (y del milenio anterior, claro) a no desarrollar casi nada nuevo referente a la ciencia, sino básicamente analizar una y otra vez los detalles de la obra de Aristóteles. El italiano está convencido de que la verdad se encuentra mirando al mundo, y no sólo a los libros escritos milenios antes, y como siempre, nos lo deja caer en voz de uno de sus personajes.

Salviati – Así será, ya que así lo deseáis. La primera pregunta era, ¿cómo puede ser un solo punto igual a una línea? Ya que no puedo hacer más ahora mismo intentaré eliminar, o al menos disminuir, una improbabilidad introduciendo una similar o tal vez más grande, del mismo modo que a veces una maravilla es eclipsada por un milagro.

Haré esto mostrándoos dos superficies idénticas, junto con dos sólidos iguales que tienen como base estas superficies, y haciendo que los cuatro disminuyan de tamaño de manera continua y uniforme de modo que siempre mantengan la igualdad entre ellos; finalmente tanto las superficies como los sólidos dejarán de ser iguales degenerando, un sólido y una superficie en un segmento muy largo, y el otro sólido y la otra superficie en un único punto; dicho de otro modo, los segundos se convertirán en un punto y los primeros en un número infinito de puntos.

En un momento veremos el detalle del razonamiento de Galileo, pero observa la técnica básica que tiene para aproximarse al concepto de infinito: no compara infinitos de golpe, sino que lo hace a partir de límites. Parte de valores finitos y razonables, y no da ningún salto sino que se aproxima gradualmente al infinito; aunque hoy en día tengamos unas matemáticas mucho más sofisticadas que él, el paso conceptual que da el italiano es tremendo.

Sagredo – Esta propuesta parece, efectivamente, maravillosa; pero escuchemos su explicación y demostración.

¡Ojo! Aunque la descripción de Galileo es clara, es farragosa: hace falta ir mirando la figura para ver los puntos y segmentos de los que habla. Pero, cuando lo hagas, verás que tampoco era para tanto y es relativamente fácil visualizar lo que dice.

Salviati – Ya que la demostración es puramente geométrica necesitaremos una figura. Sea AFB una semicircunferencia con centro en C; describamos a su alrededor el rectángulo ADEB y, desde el centro, tracemos los segmentos CD y CE hasta los puntos D y E. Sea CF el radio perpendicular tanto a AB como a DE, y supongamos que la figura completa rota alrededor de este radio como eje. Resulta evidente que el rectángulo ADEB describirá entonces un cilindro, la semicircunferencia AFB una semiesfera, y el triángulo CDE un cono.

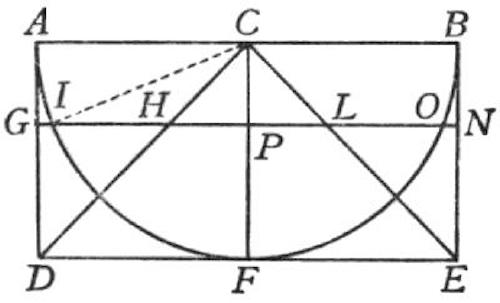
Figura 6.

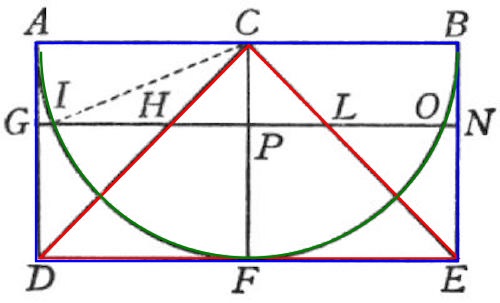
Figura 6 con las tres formas en colores diferentes.

Otro aviso: aunque Galileo es magistral, es desordenado. A continuación va a decirnos todo lo que pretende demostrar con esa figura, como si fuera una lista de objetivos a conseguir, pero lo que vas a leer no es la demostración todavía. Por lo tanto, que no te impresione la lista de demostraciones a realizar y, si no entiendes algún detalle, no te preocupes lo más mínimo porque luego volveremos a ello poco a poco, cuando realmente lo demuestre.

A continuación eliminemos la semiesfera pero dejemos el cono y el resto del cilindro, los cuales, por su forma, llamaremos un “cuenco”. En primer lugar vamos a demostrar que el cuenco y el cono son iguales; a continuación demostraremos que un plano paralelo a la circunferencia que forma la base del cuenco y que tiene como diámetro el segmento DE y como centro F –un plano cuya traza es GN– corta al cuenco en los puntos G, I, O y N, y al cono en los puntos H y L, de modo que la parte del cono señalada como CHL siempre es igual a la parte del cuenco cuyo perfil se representa mediante los triángulos GAI y BON.

La traza de un plano es la línea de intersección con otro de proyección, en este caso vertical. La traza de la que habla Galileo es el corte del plano horizontal que pasa por G, P y N con el plano vertical definido por ABDE. Esa traza es el segmento GN.

Además, demostraremos que la base del cono, es decir, el círculo de diámetro HL, es igual que la superficie circular que forma la base de esta parte del cuenco o, podríamos decir, igual que un lazo cuya anchura es GI. (Observad, por cierto, la naturaleza de las definiciones matemáticas que consisten simplemente en imponer nombres o, si lo preferís, abreviar el discurso de un modo establecido e introducido para evitar el aburrimiento que sufriríamos vosotros yo si no hubiéramos acordado denominar a esta superficie “banda circular” y a la parte afilada del borde del cuenco “filo redondo”).

Ahora bien, llamémoslas como deseéis, es suficiente con comprender que un plano trazado a cualquier altura, siempre que sea paralelo a la base, es decir, al círculo de diámetro DE, siempre cortará a los dos sólidos de modo que la porción del cono CHL será igual que la porción superior del cuenco; del mismo modo, las dos áreas que son las bases de estos sólidos –es decir, la banda y el círculo HL– son también iguales. Aquí tenemos el milagro mencionado antes: según el plano se acerca hacia el borde superior, las porciones de los dos sólidos siempre son iguales, y también lo son las áreas de sus bases.

Insisto: aunque Galileo diga que es suficiente con comprender esto, no lo ha demostrado aún. Lo hará cuando, afortunadamente, uno de sus contertulios lo empuje a hacerlo. No es obvio –al menos, no para mí–, sin más explicación, que lo que el italiano dice que es igual lo sea. Paciencia.

Y cuando el plano secante alcanza el borde superior, los dos sólidos –siempre iguales–, lo mismo que sus bases –áreas también idénticas– finalmente se desvanecen, de modo que un par degenera hasta convertirse en una circunferencia y el otro par en un punto único, el filo redondo del cuenco en un caso y el vértice del cono en el otro. Ahora bien, dado que según estos sólidos disminuyen de tamaño siempre se mantiene la igualdad entre ellos hasta el final, estamos justificados en afirmar que, en el extremo final de esta disminución, siguen siendo iguales, y que uno de ellos no es infinitamente más grande que el otro. Parece, por lo tanto, que podemos igualar la circunferencia de un gran círculo con un único punto.

Pero esto que es cierto de los sólidos también lo es de las superficies que forman sus bases; porque ellas también mantienen su igualdad a lo largo de la disminución de tamaño, y al final se desvanecen, la primera en forma de circunferencia y la otra en forma de un único punto. ¿No podemos llamarlas iguales, viendo que son los últimos restos de entes de igual magnitud?

Fijaos también en que, incluso si estos objetos fueran tan grandes que pudieran contener inmensos hemisferios celestes, tanto sus bordes superiores como los vértices de los conos contenidos en ellos siempre se mantendrían con igual tamaño y se desvanecerían, los primeros en circunferencias con el tamaño de las más grandes órbitas celestiales, los segundos en simples puntos. Por lo tanto, de acuerdo con todo esto, podemos afirmar que todas las circunferencias, por diferentes que sean, son iguales unas a otras, y son todas iguales a un único punto.

Insisto: aunque Galileo aún no ha demostrado nada, nos deja bien claro su objetivo como aproximación al infinito. Si es capaz de demostrar que dos figuras tienen la misma extensión, y luego las disminuye proporcionalmente de manera que mantengan en todo momento la misma extensión, en el límite –cuando ambas se colapsan a figuras diferentes–, dado que han mantenido sus extensiones iguales, las figuras finales deben ser equivalentes.

Pero hace falta que Sagredo lo espolee a demostrarlo de veras:

Sagredo – Esta explicación me parece tan inteligente y novedosa que, aunque fuera capaz, no desearía oponerme a ella; pues desfigurar una estructura tan bella mediante un ataque burdo y pedante no sería sino pecaminoso. Pero, para nuestra completa satisfacción, por favor, muéstranos esta demostración geométrica de que siempre se mantiene la igualdad entre estos sólidos y entre sus bases. Pues estoy seguro de que es muy ingeniosa, viendo la sutileza del argumento filosófico basado en este resultado.

Ahora sí, Galileo demostrará lo que quiere decir con esta equivalencia entre figuras geométricas. Para hacer la explicación más clara, repetiré la figura original con

Salviati – La demostración es corta y sencilla. Refiriéndonos a la figura anterior, ya que IPC es un triángulo rectángulo, el cuadrado del radio IC es igual a la suma de los cuadrados de los dos catetos IP, PC; pero el radio IC es igual a AC y también a GP, mientras que CP es igual a PH. Por lo tanto, el cuadrado del segmento GP es igual a los cuadrados de IP y PH o, si multiplicamos todo por 4, el cuadrado del diámetro GN es igual a la suma de los cuadrados de IO y HL.

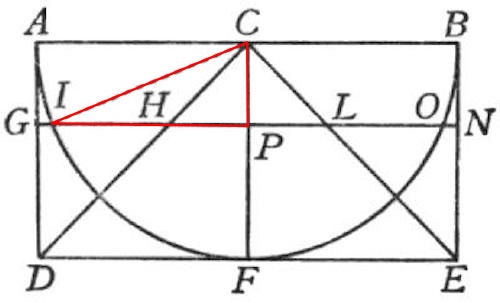
El triángulo rectángulo IPC.

Analicemos esto paso por paso. El triángulo IPC es, efectivamente, rectángulo, luego se cumple en él el teorema de Pitágoras: el cuadrado de su hipotenusa es igual a la suma de los cuadrados de sus lados: $IC^2 = IP^2 + PC^2$.

Pero, dado que IC es el radio de la semicircunferencia, lo mismo que AC, $IC = AC$. Y puesto que ACGP es un rectángulo, AC = GP. De modo que en la expresión anterior podemos poner GP en vez de IC: $GP^2 = IP^2 + PC^2$.

La otra sustitución es la siguiente: el rectángulo grande ABDE está formado por dos cuadrados idénticos, ACDF y CBFE, cada uno de los cuales contiene un cuarto de circunferencia. Por tanto, las dos diagonales DC y CE son diagonales de dos cuadrados, y forman exactamente 45 grados con la horizontal. Esto significa que, en la parte de arriba, CP es igual que PH.

Por esto, podemos escribir PH en vez de CP en la expresión de antes: $GP^2 = IP^2 + PH^2$. Pero Galileo quiere cambiarla un poquito más: multiplica toda la expresión por 4, con lo que queda $4GP^2 = 4IP^2 + 4PH^2$. Pero dado que 4 es el cuadrado de 2, podemos escribirla como $(2GP)^2 = (2IP)^2 + (2PH)^2$.

Finalmente, el italiano busca los valores de 2GP, 2IP y 2PH en la figura. 2GP es el diámetro de la semicircunferencia, es decir, GN. 2IP es lo mismo que IO, ya que $IP = PO$, y 2PH es lo mismo que HL, porque $PH = PL$.

Con todo esto, la expresión final a la que llega Galileo es $GN^2 = IO^2 + HL^2$. ¿Que por qué esto es más interesante que la expresión original? Para eso tienes que esperar un instante más, pero útil o no, espero que haya quedado claro que la expresión a la que hemos llegado es verdadera.

Dado que las áreas de los círculos son proporcionales a los cuadrados de sus diámetros, se deduce que el área del círculo de diámetro GN es igual a la suma de las áreas de los círculos de diámetros IO y HL, de modo que si eliminamos el área común del círculo de diámetro IO, la superficie restante del círculo GN será igual a la del círculo de diámetro HL. Con esto está demostrada la primera parte.

Sabíamos que $GN^2 = IO^2 + HL^2$. Pero, si multiplicamos toda la expresión por $\pi$, tenemos $\pi GN^2 = \pi IO^2 + \pi HL^2$. Ahora bien, el producto de $\pi$ por el diámetro de una circunferencia nos da el área del círculo. Lo que esto significa es que el área del círculo de diámetro GN es igual a la suma del área del círculo de diámetro IO más el área del círculo de diámetro HL.

Recuerda que esos círculos no están en el plano del papel, sino que son el resultado de hacer girar la figura alrededor del eje CF. El círculo de radio HL es la base del cono cuyo vértice está en C, el círculo de diámetro GN es la base del cilindro y el círculo de diámetro IO es el “hueco” que queda dentro del cuenco. No es fácil representar esto en tres dimensiones, pero es posible que esta figura te ayude a ver los tres círculos de los que habla Galileo:

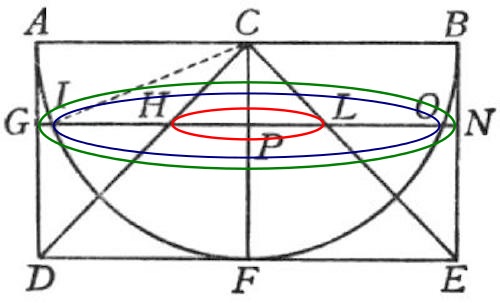
Los tres círculos en brega.

De modo que el área del círculo verde es igual a la suma de las áreas de los otros dos. Pero lo interesante no es eso: es que, si eso es así, el área del círculo rojo es la diferencia entre las áreas del verde y el azul. Y dado que el círculo verde es todo el cilindro, y el círculo azul es el del hueco, el área que queda en los “rebordes” GI y ON es exactamente igual que el área del círculo rojo. En la siguiente figura, las dos áreas rojas son iguales:

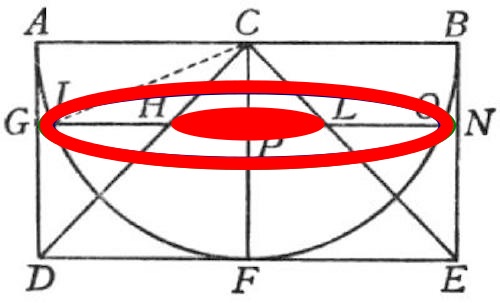
Las dos áreas iguales.

Y ahora Galileo, aunque haya dejado de decirlo porque creo que da por sentado que el lector lo razonará solo, hace el paso al límite. Ha hecho este razonamiento con la línea horizontal GN a cierta altura. ¿Qué cambiaría si la subimos un poco?

Todas las expresiones que hemos obtenido seguirían siendo válidas, es decir, las dos áreas rojas seguirían siendo iguales. Ambas serían, sin embargo, más pequeñas al subir la línea horizontal de “base”. ¿Qué sucede en el límite?

Que la base del cono se colapsa a un solo punto: el vértice C. Y que la anchura de la banda exterior se desvanece, hasta que en el límite (al llevar GN a AB) su anchura es nula y se ha colapsado a una circunferencia.

Por lo tanto, el razonamiento de Galileo es el siguiente: ambas figuras mantienen exactamente igual su extensión en todo momento, como hemos demostrado, y finalmente una se convierte en un punto y la otra en una circunferencia. Por tanto, un punto y una circunferencia son equivalentes y uno de ellos no tiene más extensión que el otro.

Sé que esto es cuestionable por muchísimas razones –entre otras, hablar de la extensión de un punto y una línea–, pero lo absolutamente revolucionario del italiano es la aproximación al misterio del infinito haciendo un auténtico límite, no simplemente unos cuantos pasos, y demostrando que incluso cuando algo se hace infinitamente grande o pequeño es posible que haya magnitudes que permanezcan constantes. Desde luego, esta conclusión le supondrá en un momento verdaderos dilemas.

Respecto a la segunda, dejaremos su demostración por ahora, en parte porque quienes deseen seguirla pueden encontrarla en la proposición decimosegunda del segundo libro De centro gravitatis solidorum del Arquímedes de nuestra era, Luca Valerio, que la empleó con un propósito diferente; y por otra parte ya que, para nuestro propósito, es suficiente con ver que las superficies antes mencionadas son siempre iguales y que, según disminuyen de tamaño uniformemente, degeneran una de ellas en un único punto y la otra en una circunferencia más fina que cualquiera que podamos imaginar; aquí estriba nuestro milagro.

Sagredo – La demostración es ingeniosa, y las conclusiones que se derivan de ella, notables. Y ahora cuéntanos algo sobre la otra duda presentada por Simplicio, si es que tienes algo especial que decir, lo cual me parece sin embargo harto improbable, puesto que el asunto ha sido ya discutido en gran profundidad.

La otra duda presentada por Simplicio era la siguiente, planteada en el fragmento anterior:

Simplicio – Además, esta construcción de segmentos a partir de puntos, divisibles a partir de indivisibles, y finitos a partir de infinitos, me produce una duda muy difícil de evitar.

De modo que eso es lo que el italiano pretende atacar a continuación, y lo llevará a una paradoja matemática maravillosa que lleva su nombre:

Salviati – Pues sí tengo algo especial que decir, y en primer lugar repetiré lo que ya dije antes, a saber, que la infinitud y la indivisibilidad son, por su propia naturaleza, incomprensibles para nosotros; imaginad entonces lo que se convierten al combinarlas. Ahora bien, si queremos construir una línea de puntos indivisibles necesitamos un número infinito de ellos y, por lo tanto, deberemos entender tanto lo infinito como lo indivisible al mismo tiempo.

Se han pasado muchas ideas por mi cabeza a este respecto, algunas de las cuales –seguramente las más importantes– tal vez no pueda recordar a bote pronto; pero en el curso de nuestra discusión tal vez consiga despertar en vosotros, y especialmente en Simplicio, objeciones y dudas que a su vez traerán a mi memoria lo que, sin ese estímulo, hubiera permanecido dormido en mi mente. Permitidme por lo tanto la libertad habitual de presentaros algunas de nuestras ocurrencias humanas, porque así deberíamos llamarlas en comparación con la verdad sobrenatural sobre la que se asienta el único recurso seguro y fiable para tomar decisiones en nuestras sicusiones, y que es una guía infalible en los caminos oscuros y dudosos del pensamiento.

Una de las principales objeciones que se han presentado a esta construcción de continuos a partir de indivisibles es que la adición de un indivisible a otro nunca puede producir un divisible, porque si así fuere lo indivisible se convertiría en divisible. Así si dos indivisibles –por ejemplo, dos puntos– pueden unirse para formar una línea divisible, entonces podría formarse una línea más larga uniendo tres, cinco, siete o cualquier número impar de puntos. Pero dado que estas líneas pueden dividirse en dos segmentos iguales, se hace posible dividir lo indivisible que está justo en el centro de la línea. En respuesta a esto y a otras objeciones del mismo tipo responderé que una magnitud divisible nunca puede ser construida a partir de dos o diez o cien o mil indivisibles, sino que requiere un número infinito de ellos.

Dicho de otro modo: con un número finito de puntos –que Galileo llama “indivisibles”– no es posible formar un segmento de ninguna longitud –un “divisible”–, por pequeña que sea. Es necesario un número infinito de indivisibles para formar un divisible.

Pero lo raro aquí, claro está, es lo siguiente: si para hacer un segmento de un centímetro de longitud hacen falta infinitos puntos, y para hacer uno de cien kilómetros de longitud también hacen falta infinitos puntos, ¿en cuál de los dos segmentos hay más puntos? ¿todos los infinitos son iguales? Si así fuese, ambos segmentos tendrían el mismo número de puntos, lo cual es extraño. Pero si no fuera así, ¿cómo se comparan infinitos?

Afortunadamente para nosotros, Simplicio, como casi siempre, hace de nuestra boca:

Simplicio – Aquí aparece una duda que me parece irresoluble. Ya que está claro que podemos tener un segmento más largo que otro, cada uno compuesto por un número infinito de puntos, debemos admitir que dentro de una clase podemos tener algo más grande que infinito, ya que la infinidad de puntos del segmento más largo es mayor que la infinidad de puntos del más corto. Esta asignación a una cantidad infinita de un valor mayor que infinito está completamente fuera de mi comprensión.

Salviati – Éste es uno de los obstáculos que surgen cuando intentamos, con nuestras mentes finitas, discutir sobre el infinito, asignándole las propiedades que otorgamos a lo finito y limitado; pero creo que esto es un error, pues no podemos hablar de que una cantidad infinita es mayor o menor que otra. Para demostrar esto tengo en mente un argumento que, para mayor claridad, expondré como una serie de preguntas a Simplicio, ya que ha sido él quien ha presentado esta objeción.

Doy por sentado que sabes qué números son cuadrados y cuáles no.

En términos más modernos, cuando Galileo habla de números cuadrados quiere decir cuadrados perfectos.

Simplicio – Soy muy consciente de que un cuadrado es un número que resulta de la multiplicación de otro número por sí mismo; así 4, 9, etc., son cuadrados perfectos que provienen de la multiplicación de 2, 3, etc., por sí mismos.

Salviati – Muy bien; y también sabes que lo mismo que estos productos se llaman cuadrados, sus factores se denominan lados o raíces; mientras que los números que no consisten en un producto de dos factores iguales no son cuadrados. Por lo tanto, si afirmo que todos los números, incluyendo tanto cuadrados como no cuadrados, son más que los cuadrados, diré la verdad, ¿no es así?

Simplicio – Indudablemente.

Esto es lógico: algunos números son cuadrados perfectos, y otros no lo son. Por lo tanto, la totalidad de los números es mayor que la de los cuadrados perfectos, que son un subconjunto de ellos.

Salviati – Y si a continuación pregunto cuántos cuadrados hay, responderíamos acertadamente si decimos que hay tantos como su correspondiente número de raíces, puesto que cada cuadrado tiene su propia raíz y cada raíz su propio cuadrado, y no hay ningún cuadrado con más de una raíz ni ninguna raíz con más de un cuadrado.

Simplicio – Exactamente.

Es posible que veas hacia dónde va Galileo: en primer lugar hemos establecido sin lugar a dudas que hay más números que cuadrados perfectos. Pero luego hemos visto que hay una relación de uno a uno entre ellos: no hay ningún número sin su cuadrado, ni ningún cuadrado perfecto sin su raíz.

Salviati – Pero si me pregunto cuántas raíces hay, no podemos negar que hay tantas raíces como números, porque todo número es raíz de algún cuadrado. Al ser esto así, debemos afirmar que hay tantos cuadrados como números, ya que hay tantos cuadrados como raíces y todos los números son raíces. Pero al principio dijimos que hay muchos más números que cuadrados, ya que la mayor parte de ellos no son cuadrados. No sólo eso, sino que la proporción de cuadrados disminuye según nos movemos hacia números más grandes. Así, hasta el 100 hay 10 cuadrados, es decir, los cuadrados constituyen la 1/10 parte de todos los números; hasta 10 000 encontramos una fracción de sólo 1/100 de cuadrados; y hasta un millón, sólo la 1/1 000 parte. Pero al mismo tiempo en un número infinito, si pudiéramos concebirlo, estaríamos forzados a admitir que hay tantos cuadrados como números en total.

Sagredo – Pero ¿a qué conclusión podemos llegar entonces, en estas circunstancias?

Salviati – En mi opinión sólo podemos deducir que la totalidad de todos los números es infinita, que el número de cuadrados es infinito y que el número de sus raíces es infinito; ni es el número de cuadrados menor que el de todos los números, ni es el segundo mayor que el primero. Y, finalmente, que los atributos “igual”, “mayor” y “menor” no son aplicables a las magnitudes infinitas, sino sólo a las finitas.

Esto no es cierto: sí es posible comparar infinitos, y no son todos iguales, sino que unos son mayores que otros. Sin embargo, harían falta siglos de desarrollo de las Matemáticas para que nos diéramos cuenta de ello.

Lo que Galileo plantea en este fragmento es una paradoja matemática muy famosa, llamada naturalmente paradoja de Galileo: hay más números naturales que cuadrados perfectos, pero no hay ningún número natural que no tenga un cuadrado correspondiente.

La paradoja fue resuelta en el siglo XIX por un genio matemático muy superior al de Galileo: Georg Cantor estableció una teoría de conjuntos infinitos que permitía comparar lo que el italiano no había podido. Pero claro, estamos hablando de doscientos años después.

Así, cuando Simplicio menciona segmentos de diferentes longitudes y me pregunta cómo es posible que los más largos no tengan más puntos que los más cortos, le respondo que un segmento no tiene más o menos ni el mismo número de puntos que otro, sino que cada uno tiene un número infinito. O, si le hubiera respondido que los puntos de un segmento son tantos como los cuadrados; de otro, mayor que todos los números; y en el más corto tantos como el número de cubos, ¿no podría satisfacer su duda poniendo más puntos en una línea que en otra manteniendo un número infinito en cada una? No hay más que decir de la primera duda.

Y de la segunda hablaremos en el siguiente fragmento, porque no me negarás que éste ha sido intenso. ¡Hasta entonces, descansa las neuronas!